Customizing Figure Layouts Using GridSpec and Other Functions

How to create grid-shaped combinations of axes.

subplots()

Perhaps the primary function used to create figures and axes. It’s also similar to subplot(), but creates and places all axes on the figure at once.

GridSpec

Specifies the geometry of the grid that a subplot will be placed. The number of rows and number of columns of the grid need to be set. Optionally, the subplot layout parameters (e.g., left, right, etc.) can be tuned.

SubplotSpec

Specifies the location of the subplot in the given GridSpec.

subplot2grid()

A helper function that is similar to subplot(), but uses 0-based indexing and let subplot to occupy multiple cells. This function is not covered in this tutorial.

import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec

Basic Quickstart Guide

These first two examples show how to create a basic 4-by-4 grid using both subplots() and gridspec.

Using subplots() is quite simple. It returns a Figure instance and an array of Axes objects.

fig1, f1_axes = plt.subplots(ncols=2, nrows=2)
fig1.tight_layout()

For a simple use case such as this, gridspec is perhaps overly verbose. You have to create the figure and GridSpec instance separately, then pass elements of gridspec instance to the add_subplot() method to create the axes objects. The elements of the gridspec are accessed in generally the same manner as numpy arrays.

fig2 = plt.figure()
spec2 = gridspec.GridSpec(ncols=2, nrows=2)
f2_ax1 = fig2.add_subplot(spec2[0, 0])
f2_ax2 = fig2.add_subplot(spec2[0, 1])
f2_ax3 = fig2.add_subplot(spec2[1, 0])
f2_ax4 = fig2.add_subplot(spec2[1, 1])
fig2.tight_layout()

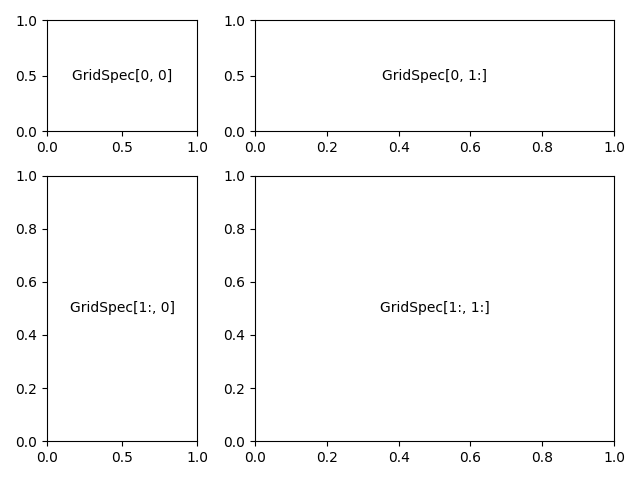
When you want to have subplots of different sizes, however, gridspec becomes indispensable and provides a couple of options. The method shown here initializes a uniform grid specification, and then uses typical numpy indexing and slices to allocate multiple “cells” for a given subplot.

fig3 = plt.figure()
spec3 = gridspec.GridSpec(ncols=3, nrows=3)
anno_opts = dict(xy=(0.5, 0.5), xycoords='axes fraction',
                 va='center', ha='center')

fig3.add_subplot(spec3[0, 0]).annotate('GridSpec[0, 0]', **anno_opts)
fig3.add_subplot(spec3[0, 1:]).annotate('GridSpec[0, 1:]', **anno_opts)
fig3.add_subplot(spec3[1:, 0]).annotate('GridSpec[1:, 0]', **anno_opts)
fig3.add_subplot(spec3[1:, 1:]).annotate('GridSpec[1:, 1:]', **anno_opts)

fig3.tight_layout()

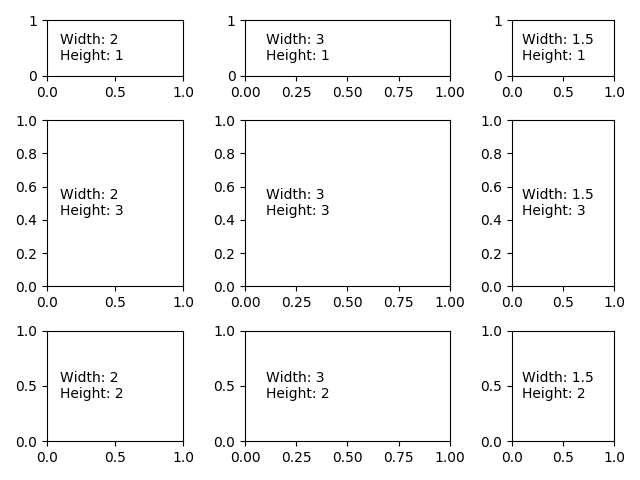
Other option is to use the width_ratios and height_ratios parameters. These keyword arguments are lists of numbers. Note that absolute values are meaningless, only their relative ratios matter. That means that width_ratios=[2, 4, 8] is equivalent to width_ratios=[1, 2, 4] within equally wide figures. For the sake of demonstration, we’ll blindly create the axes within for loops since we won’t need them later.

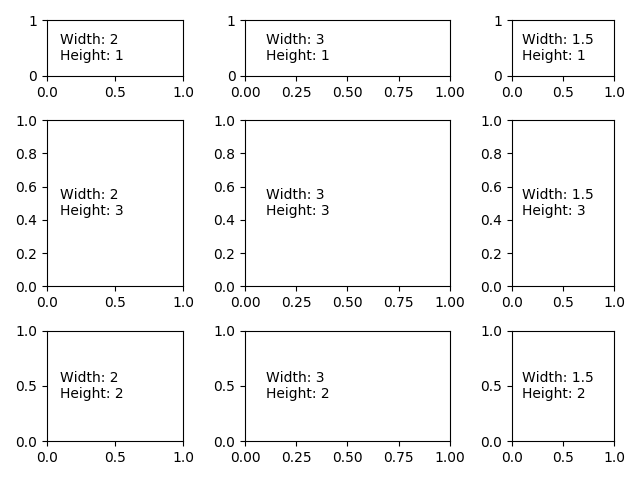
fig4 = plt.figure()
widths = [2, 3, 1.5]
heights = [1, 3, 2]
spec4 = gridspec.GridSpec(ncols=3, nrows=3, width_ratios=widths,
                          height_ratios=heights)
for row in range(3):
    for col in range(3):
        ax = fig4.add_subplot(spec4[row, col])
        label = 'Width: {}\nHeight: {}'.format(widths[col], heights[row])
        ax.annotate(label, (0.1, 0.5), xycoords='axes fraction', va='center')

fig4.tight_layout()

Learning to use width_ratios and height_ratios is particularly useful since the top-level function subplots() accepts them within the gridspec_kw parameter. For that matter, any parameter accepted by GridSpec can be passed to subplots() via the gridspec_kw parameter. This example recreates the previous figure without directly using a gridspec instance.

gs_kw = dict(width_ratios=widths, height_ratios=heights)
fig5, f5_axes = plt.subplots(ncols=3, nrows=3, gridspec_kw=gs_kw)
for r, row in enumerate(f5_axes):
    for c, ax in enumerate(row):
        label = 'Width: {}\nHeight: {}'.format(widths[c], heights[r])
        ax.annotate(label, (0.1, 0.5), xycoords='axes fraction', va='center')

fig5.tight_layout()

Fine Adjustments to a Gridspec Layout

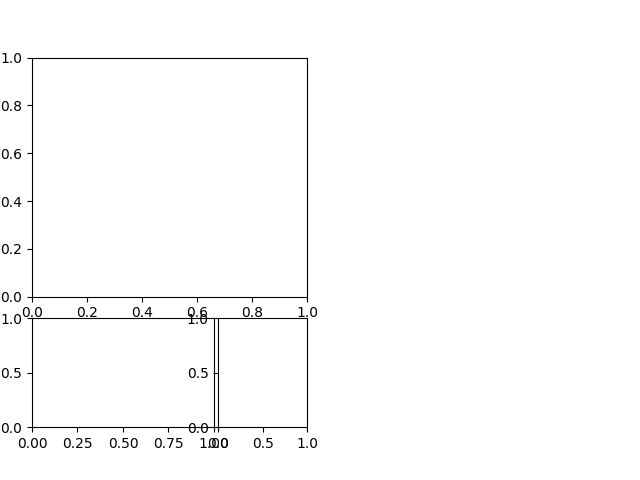
When a GridSpec is explicitly used, you can adjust the layout parameters of subplots that are created from the GridSpec.

fig = plt.figure()
gs1 = gridspec.GridSpec(nrows=3, ncols=3, left=0.05, right=0.48, wspace=0.05)
ax1 = fig.add_subplot(gs1[:-1, :])
ax2 = fig.add_subplot(gs1[-1, :-1])
ax3 = fig.add_subplot(gs1[-1, -1])

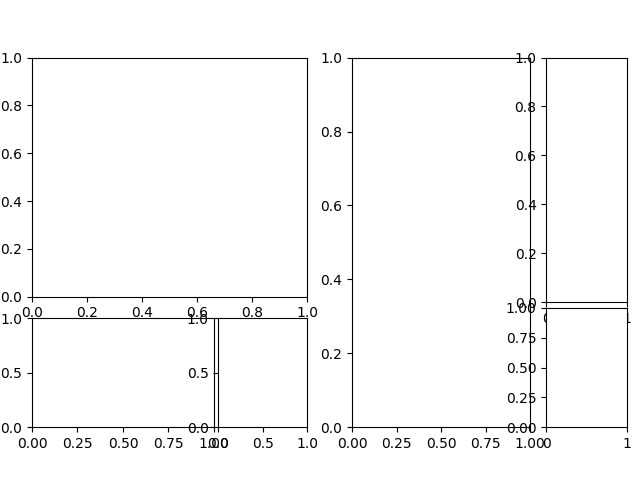
This is similar to subplots_adjust(), but it only affects the subplots that are created from the given GridSpec.

For example, compare the left and right sides of this figure:

fig = plt.figure()
gs1 = gridspec.GridSpec(nrows=3, ncols=3, left=0.05, right=0.48,
                        wspace=0.05)
ax1 = fig.add_subplot(gs1[:-1, :])
ax2 = fig.add_subplot(gs1[-1, :-1])
ax3 = fig.add_subplot(gs1[-1, -1])


gs2 = gridspec.GridSpec(nrows=3, ncols=3, left=0.55, right=0.98,
                        hspace=0.05)
ax4 = fig.add_subplot(gs2[:, :-1])
ax5 = fig.add_subplot(gs2[:-1, -1])
ax6 = fig.add_subplot(gs2[-1, -1])

GridSpec using SubplotSpec

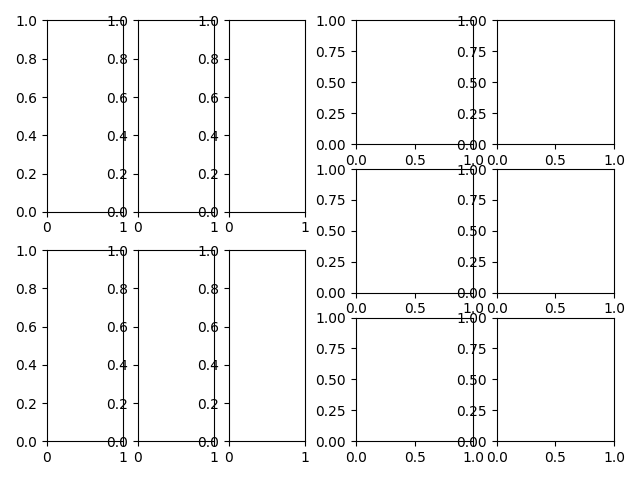
You can create GridSpec from the SubplotSpec, in which case its layout parameters are set to that of the location of the given SubplotSpec.

fig = plt.figure()
gs0 = gridspec.GridSpec(1, 2)

gs00 = gridspec.GridSpecFromSubplotSpec(2, 3, subplot_spec=gs0[0])
gs01 = gridspec.GridSpecFromSubplotSpec(3, 2, subplot_spec=gs0[1])

for a in range(2):
    for b in range(3):
        fig.add_subplot(gs00[a, b])
        fig.add_subplot(gs01[b, a])

fig.tight_layout()

A Complex Nested GridSpec using SubplotSpec

Here’s a more sophisticated example of nested GridSpec where we put a box around each cell of the outer 4x4 grid, by hiding appropriate spines in each of the inner 3x3 grids.

import numpy as np
from itertools import product


def squiggle_xy(a, b, c, d, i=np.arange(0.0, 2*np.pi, 0.05)):
    return np.sin(i*a)*np.cos(i*b), np.sin(i*c)*np.cos(i*d)

fig = plt.figure(figsize=(8, 8))

# gridspec inside gridspec
outer_grid = gridspec.GridSpec(4, 4, wspace=0.0, hspace=0.0)

for i in range(16):
    inner_grid = gridspec.GridSpecFromSubplotSpec(
      3, 3, subplot_spec=outer_grid[i], wspace=0.0, hspace=0.0)
    a, b = int(i/4)+1, i % 4+1
    for j, (c, d) in enumerate(product(range(1, 4), repeat=2)):
        ax = plt.Subplot(fig, inner_grid[j])
        ax.plot(*squiggle_xy(a, b, c, d))
        ax.set_xticks([])
        ax.set_yticks([])
        fig.add_subplot(ax)

all_axes = fig.get_axes()

# show only the outside spines
for ax in all_axes:
    for sp in ax.spines.values():
        sp.set_visible(False)
    if ax.is_first_row():
        ax.spines['top'].set_visible(True)
    if ax.is_last_row():
        ax.spines['bottom'].set_visible(True)
    if ax.is_first_col():
        ax.spines['left'].set_visible(True)
    if ax.is_last_col():
        ax.spines['right'].set_visible(True)

plt.show()

Total running time of the script: ( 0 minutes 13.979 seconds)