Version 2.0.0b1.post7580.dev0+ge487118

Demonstrate the Sankey class by producing three basic diagrams.
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.sankey import Sankey
Example 1 – Mostly defaults
This demonstrates how to create a simple diagram by implicitly calling the Sankey.add() method and by appending finish() to the call to the class.
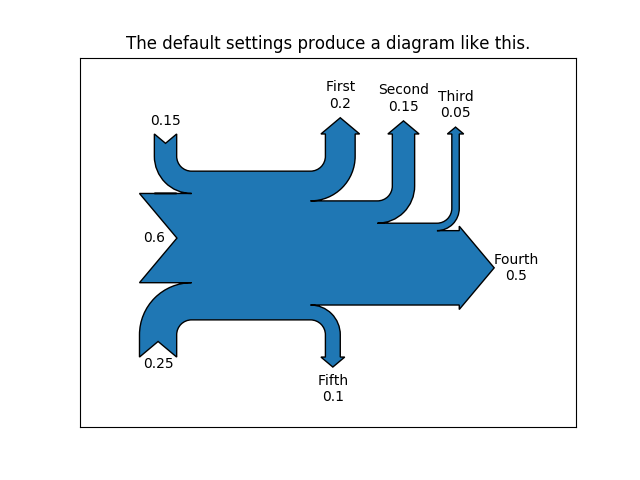
Notice:
Example 2
This demonstrates:
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1, xticks=[], yticks=[],
title="Flow Diagram of a Widget")
sankey = Sankey(ax=ax, scale=0.01, offset=0.2, head_angle=180,
format='%.0f', unit='%')
sankey.add(flows=[25, 0, 60, -10, -20, -5, -15, -10, -40],
labels=['', '', '', 'First', 'Second', 'Third', 'Fourth',
'Fifth', 'Hurray!'],
orientations=[-1, 1, 0, 1, 1, 1, -1, -1, 0],
pathlengths=[0.25, 0.25, 0.25, 0.25, 0.25, 0.6, 0.25, 0.25,
0.25],
patchlabel="Widget\nA") # Arguments to matplotlib.patches.PathPatch()
diagrams = sankey.finish()
diagrams[0].texts[-1].set_color('r')
diagrams[0].text.set_fontweight('bold')
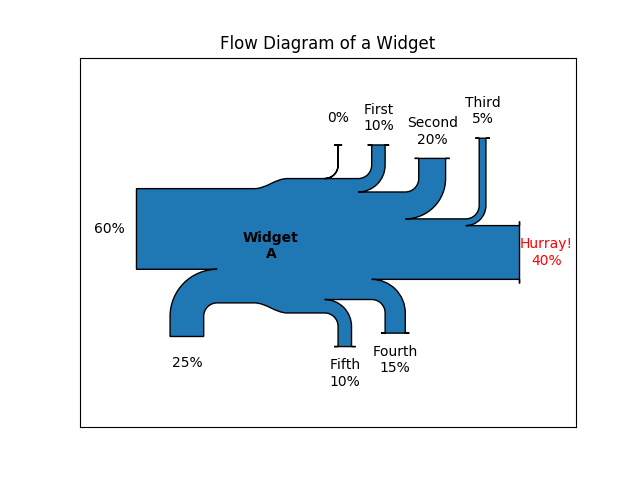
Notice:
Example 3
This demonstrates:
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1, xticks=[], yticks=[], title="Two Systems")
flows = [0.25, 0.15, 0.60, -0.10, -0.05, -0.25, -0.15, -0.10, -0.35]
sankey = Sankey(ax=ax, unit=None)
sankey.add(flows=flows, label='one',
orientations=[-1, 1, 0, 1, 1, 1, -1, -1, 0])
sankey.add(flows=[-0.25, 0.15, 0.1], label='two',
orientations=[-1, -1, -1], prior=0, connect=(0, 0))
diagrams = sankey.finish()
diagrams[-1].patch.set_hatch('/')
plt.legend(loc='best')
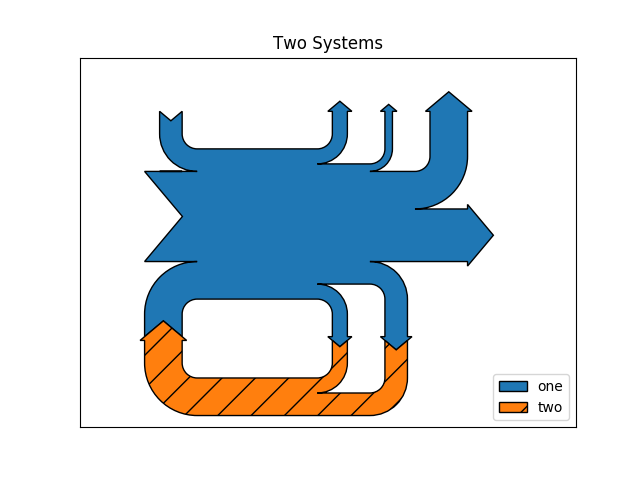
Notice that only one connection is specified, but the systems form a circuit since: (1) the lengths of the paths are justified and (2) the orientation and ordering of the flows is mirrored.
plt.show()